主専攻実験：
3DCGソフトウェアを用いたパラメトリック形状モデリング

担当教員

三谷　純　mitani＠cs.tsukuba.ac.jp ( 内線2333, 総合研究棟B棟906 )

実施学期・実施場所

春学期・総合研究棟B棟925

連絡事項

令和6年度 第1回目（4月24日 3限）を 総合研究棟B棟925で行います。

実験の目的

1. パラメータ操作によって決定される3D幾何形状のモデリングを行う
2. 幾何形状のアニメーション表示を行なう
3. （オプション）幾何形状を3Dプリンタ・レーザーカッターなどを利用してソフトウェアで生成した形状モデルの実体化を行う

2023年度 受講生の作例（切頂20面体の展開）

使用機材等

• ノートPCを各自持参のこと
• 3Dソフトウェア「Rhino - Rhinoceros 3D」のライセンスを貸与
• （オプション）3Dプリンタ・レーザーカッター・カッティングプロッタを使用可

実験の主旨

直方体や球、トーラスといった幾何学図形を描くために、CGおよびCADソフトウェアを使用することができます。
これらの図形は、直方体であれば (幅、高さ、奥行)という3つのパラメータ、球であれば (半径) という1つのパラメータ、そしてトーラスであれば (半径, 太さ)といった2つのパラメータで形状を決定できます。
本実験では、このような形状を決定するためのパラメータを操作することを通して、幾何学形状そのものを操作する方法を習得することを第一の目的とします。

Rhino + Grasshopperツールによるパラメータ操作と形状生成

また、CG技術のひとつの大きな役割として、実際には目で見ることができない情報を可視化することが挙げられます。
とくに数学および物理学の分野で「数式」として示されるものが、実は図形として可視化することで理解が容易になるものが多くあります。 単純な幾何にとどまらず、射影幾何、位相幾何、フラクタルなどは可視化によって理解を深めることができる具体的な例といえるでしょう。
CGによる形状モデリングの技術を、こういった数学・物理の基礎的な理解を支援するために活用する具体的な例を作り上げることを第二の目的とします。

2023年度 受講生の作例（正八面体と正二十面体間の変形アニメーション）

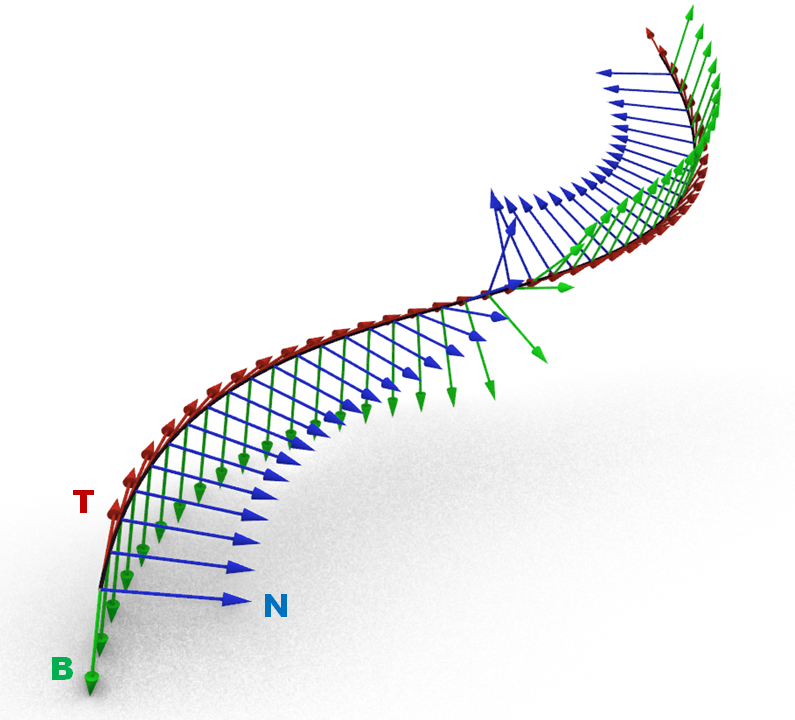
変曲点を持つ空間曲線のフレネ機構（接線・法線・従法線ベクトル）の可視化

近年では、3Dプリンタやレーザーカッターなどのデジタル加工機器の普及により、計算機上の幾何モデルを容易に実体化できるようになりました。
形状モデリングの技術と、こういったデジタル加工機器の活用によって、新しいパーソナルファブリケーション（個人によるものづくり）を体験することを第三の目的とします。

実験の概要

実験では、建築やデザイン業界で広く使われている3DCGソフトウェアであるRhinocerosを使用します。 そのプラグインであるGrasshopperでは、PythonやC#といったプログラミング言語で、形状生成のためのスクリプトを書くことができます。 これを利用して、さまざまな幾何形状および、そのアニメーション映像を作成します。また、オプションとして3Dプリンターやレーザーカッターを使用した実モデルの制作を行います。

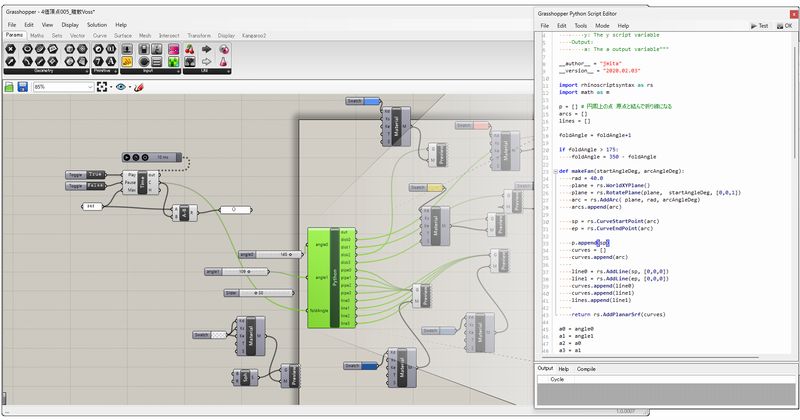
本実験は以下の３つの課題から構成されます。

(1) Rhinocerous の標準的な機能を使用した立体形状モデリング
チュートリアルを行うなどして、Rhinocerous の基本的な操作方法を修得したのち、幾何学図形の形状モデリングを行います。この課題を通して、Rhinocerous を十分に使いこなせるようにすることを目指します。また、数学的に興味深い形を探し、その特徴の理解を促すための形状モデルの作成を行います。

(2) GrasshopperとScirptを用いた立体形状モデリングとアニメーションの作成
チュートリアルを行うなどして、Grasshopper の基本的な操作方法を修得したのち、Scriptを使った形状生成手法について学びます。スクリプトによって、より複雑な形状を生成できるようになることを目指します。また、パラメータ変更によって、対象形状が変形するアニメーションの生成を行います。

つの折り目を持つ構造の折りたたみの様子（折り線の配置による動きの違いを確認できる）

折りたたみ構造への厚みの付与

(3) 最終課題
これまでの課題で学んだことをもとに自らテーマを定め、形状モデルおよびアニメーションの作成を行います。Kangarooを用いた物理シミュレーションなど、上記以外の機能をさまざまに利用して構いません。

資料

• Rhino チュートリアル（基本）
• Grasshopper チュートリアル
• RhinoとGrasshopperとPythonScriptのWiki
• CAD を使うと 数学が面白い（アイデアに困ったら）
• Math videos in order - YouTube（アイデアに困ったら）

スケジュール

実験日は15週(全28回)あります。2024年度は以下のスケジュールで行います（進捗により変更される可能性が大いにあります）

• 第1回（4/24水）：
  • ガイダンス、セットアップ
  • Rhinocerousのセットアップを行うので自分のノートPCを持参すること
  • Teamsで主専攻実験用のチームを作るので、Teamsが使えるようにしておくこと
  
  
• 第2,3回（4/26金, 5/1水）：
Rhinocerous のチュートリアルの実施


• 第4～7回（5/8水, 5/10金, 5/15水, 5/17金）
課題(1)への取り組み


• 第8回（5/17金）：
課題(1)での制作物の発表。Grasshopperの使い方説明


• 第9,10回（5/22水, 5/24金）：
Grasshopper のチュートリアル実施


• 第11～16回（5/31金, 6/5水, 6/7金, 6/12水, 6/14金, 6/19水）：
課題(2)への取り組み


• 第17回（6/21金）：
課題(2)での制作物の発表。最終課題のテーマ決め


• 第18～25週（6/26水, 6/28金, 7/3水, 7/5金, 7/10水, 7/12金, 7/17水, 7/19金）：
最終課題への取り組み


• 第26～28回（7/24水, 7/26金, 7/31水）：
最終レポート取りまとめ
7/26 成果発表

補足情報

• 普段の取り組みについて
• 毎回、授業時間終了前の20分程度を利用して、その日に行ったものの報告を Teams にて行う。
• できるだけ他の学生と交流して、互いに学び合うこと。ちょっとした操作方法については、調べるよりも教えてもらった方が圧倒的に早いことが多い。
• レポートの提出について
• 作成した作品のキャプチャ画像と、その解説を含むPDFファイル、およびRhinocerous関連ファイル一式を提出する。提出先は事前にアナウンスする。動画はmp4形式とする。

※ 過去の主専攻実験「３次元形状測定と幾何形状処理」のページ