折り紙研究ノート (三谷純)
はじめに
私は2005年前後から折り紙に対して関心を持つようになり、コンピュータグラフィックスを専門とする立場から折り紙に関する研究を行ってきました。そのなかでは主に、1枚の紙を折るだけで作れる形の設計をコンピュータで支援することを対象としてきました。

最近になり、
日本図学会の学会誌「図学研究」で折り紙に関する連載記事を書かないかというお声をかけていただきました。このWebページは、連載記事を書くに当たり、私自身がこれまでに折り紙について学んできたものを整理するとともに、できれば多くの方に私の視点から見た「折り紙」を知ってもらえればと思い作成しました。
学術的な内容は少なめにし、幅広い話題をカバーできればと思っています。
「折り紙の研究」と言った時に「いったい折り紙の何が研究になるのだろうか?」と思われる方々に、折り紙に対する新しい見方を提供できれば幸いです。
本Webページは、制作者である三谷の理解に基づいて作成されたものであり、内容に偏りがあったり、場合によっては正確でない記述があるかもしれません。お気づきの点がありましたら、遠慮なくご指摘くださいますよう、お願いいたします。よりよいものにしていきたいと思っています。掲載されている内容は適宜、追加・更新していく予定です。
私が折り紙に関する事柄を学ぶ上で、
日本折紙学会に所属される多くの方にお世話になりました。ここに感謝申し上げます。
(2012年5月)
折り紙の歴史
研究の第一歩として、対象の歴史を学ぶことは大切なことでしょう。
しかし、私自身はコンピュータサイエンスを専攻とする人間であり、一次資料にあたって折り紙の歴史を調査するようなことをしていません。
ここでは、一般的に知られている折り紙の歴史について簡単に記述するにとどめます。
「折り紙」をどのように定義するかにも依りますが、鶴や舟を折る遊戯的な折り紙が普及したのは、江戸時代初期からと考えられているようです。それ以前にも、「畳紙」や「熨斗(のし)」のような「礼法折り紙」の文化はあったようです。
世界的に origami という単語が使われるようになっていますが、ヨーロッパでも紙を折る文化は古くからありました。そのため「折り紙は日本を発祥の地として世界に広まった」という考えは正確で無いようです。
誰もが一度は折ったことがあると思われる「鶴」は江戸時代初期の作品であると考えられています。この鶴のさまざまなバリエーションをまとめた本「秘伝千羽鶴折形」が、今から200年以上も前の1797年に刊行されました。この本には、複数の鶴が連なった作品を中心に49種類もの完成図と切込みの入れ方が載っています。折り紙というと、正方形の紙を使って、切込みを入れてはいけない、と考える方が多いと思いますが、古くは自由な発想に基づいて、多くの作品が考案されていたことがうかがい知れます。この「秘伝千羽鶴折形」は、世界でもっとも古い遊戯的な折り紙の本と言われています(日本折紙学会のWebサイト
http://origami.gr.jp/SenbazuruOrikata/index.html にて各ページの写真が公開されています)。
近代的な創作折り紙が登場したのは戦後のようです。折り紙の作品を芸術の域まで高め、また新しい折り紙の基礎を築き上げた人物として、
吉澤章氏の功績は国内外で高く評価されています。
1980年前後から折り紙に「設計」の概念が導入され、さまざまに新しい折りの技法が考案されるようになりました。近年では、昆虫をはじめとする複雑な構造を持った作品が折り出されるようになっています。古典的な折り紙とは一線を画する精巧さで、折りの手数が多い複雑なものは「complex origami (コンプレックス折り紙)」とも呼ばれます。
1989年には折り紙の国際会議(現在は「折り紙の科学・数理・教育に関する国際会議:The International meeting of Origami Science, Mathematics, and Education」)が開催され、学術的な観点からの研究も進展しました。2000年以降はコンピュータの普及とともに、折り紙の設計を支援するソフトウェアや、折りによる紙の変形をシミュレーションするソフトウェアなどが多く登場するようになりました。このようなコンピュータを使った折り紙の設計・研究を指して、Computational Origamiという言葉も使用されるようになってきています。
人工衛星の太陽電池パネルの折り畳みや自動車のエアーバッグの折り畳みなど、工学分野へ折り紙の技術を活用する動きもあり、産業界へのさらなる応用が模索されています。
※1 山口真, 日本を伝える! 英語で折り紙, ナツメ社, 2005
※2
Wikipedia, 折り紙
折り紙と展開図
紙を折ってできた「形」と、紙を開いた時に残されている痕跡である「折り線」の関係についてよく観察することが折り紙について深く知る第一歩になります。
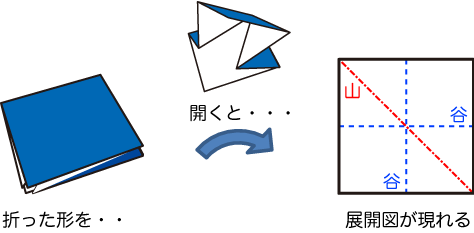
折った後の紙を開くと、そこには「山折り(Ridge fold または Mountain fold)」と「谷折り(Valley fold)」の2種類の折り線が観察できます。
この折り線の様子を図で表したものを「展開図」と呼びます。実際の折り紙作品を開くと、完成した時点では折られていない線(折り工程の途中でしるしをつけるために折られた線など)も現れますが、これらは「補助線」として区別し、展開図には含めないことが一般的です(折り手順をステップごとに図で説明したものは「折り図」と呼びます)。
展開図では、山折りを赤、谷折りを青とすることが多く(Ridge = Red でアルファベットのRつながりである、覚えるといいそうです)、色を付けない場合には山折りを一点鎖線、谷折りを破線として表すことが一般的のようで、これはなぜかペーパークラフトでみられる区別とは逆になっています。紙をひっくり返せば、山と谷が反転しますので、区別さえできれば、どちらが山でどちらが谷かにあまりこだわる必要はないのかもしれません(左右対称な形に限りますが)。
余談になりますが、折り紙では、机の上に置いた紙を手前に折る操作(谷折り)が圧倒的に多いのに対し、ペーパークラフトは立体を作る、という観点から紙を外から見て内側に折る操作(山折り)が多いです。破線、一点鎖線は「メジャーな折り方」と「マイナーな折り方」で使い分けられた、と考えるとしっくりくるかもしれません。
よく知られている折りのパターン
鶴や舟のように、何か具体的な対象物を折るのではなく、規則的なパターンを繰り返し折ることで、幾何学的に(場合によっては工学的にも)興味深い形となることがあります。
ここでは、よく知られている折りのパターンをいくつか紹介します。
蛇腹折り

山折り線と谷折り線が交互に並ぶパターンで、アコーディオンのように伸縮します。1枚の素材から接合部無しで、伸縮する機構を作れるため、加工機の防塵カバーに使用されることもあります。下の例のように、折り線を横切るような折りを新しく加えることで、より複雑なパターンを作ることができます。蛇腹折りは、折り紙設計においても、よく使われるパターンです。

蛇腹折りを横断するように2か所で折った様子
山と谷の並び方を、山・山・谷・谷とすると、トタン屋根のようになります。折り線の並びの間隔を変えたり、傾きを持たせたりすることで、さらにバリエーションを増やせます。

ミウラ折り
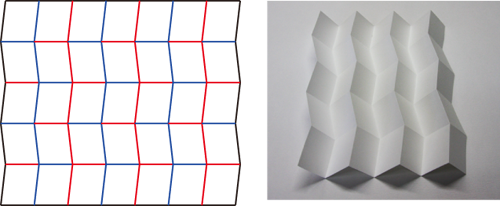
人工衛星に搭載された太陽電池パネルの折り畳みに使用されたパターンとして広く知られています。一点を固定し、他の点を移動させると全体が連動して開閉する一自由度の剛体折りパターンです。開閉が容易なことから、地図の折りたたみにも活用されています。東京大学名誉教授の三浦公亮氏の名にちなんでミウラ折りと呼ばれていますが、当の三浦先生は当初「二重波型可展構造」と呼んでいたそうです。ミウラ折りに関する詳しい情報は
MIURA-ORI GroupのWebサイト内の
「ミウラ折りの発見と科学」のコーナーで紹介されています。
吉村パターン(ダイアモンド・パターン)

円筒をつぶした時に現れるパターンと同じ構造を持ったパターンです。丸めて両端を貼りあわせることで円筒になります。この構造を深く研究された吉村慶丸氏の名前にちなんで、吉村パターンとも呼ばれるそうです。表面にこのパターンが加工された飲料缶(
ダイヤカット缶)もあります。
風船の基本形の敷き詰め

上の図は、折り紙でよく知られている「風船」を折るときに現れる基本的なパターンなので、「風船の基本形」と呼ばれています(これ以外にも、いくつかのパターンが「〜の基本形」と呼ばれています)。
三角形の辺をつなげて連結することができます。展開図は長方形になります
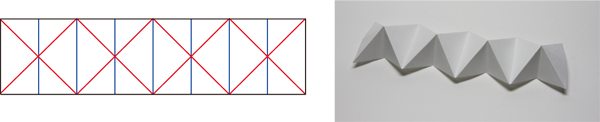
さらにこれを、基本形の半分だけずらして隣に並べていくと、下図のように面白い形になります(写真と展開図では、山と谷が反転しています)。下の展開図は、上の長方形を縦に置いて、それを横方向に4つ連結しています。この形は「Folding Techniques for Designers: From Sheet to Form (Paul Jackson著)」の表紙にも使われています。この書籍では、すでに紹介した蛇腹折りも含め、基本的な折り操作で幾何学的に美しい形を創り出す技法を多数紹介しています。

風船の基本形はいくらでも連結できるので、さらに数を増やすと次のような形になります。独立した1つの風船の基本形同様に、平らに折りたたむことができる一方で、支えがないとクルッと丸まってしまいます。両手でグニャグニャ動かすことができます。

イカロスの帆に使用されたパターン
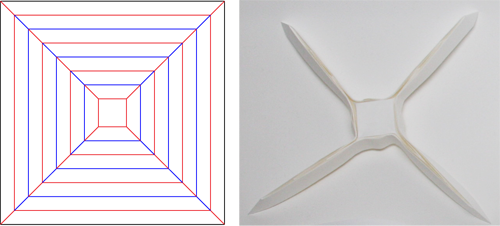
人工衛星でもロケットでも無く、どう表現するべきか難しいところですが、「世界初の宇宙ヨット」と称され、2010年に宇宙に飛び出したソーラー電力セイル機「イカロス」の薄膜太陽電池の折り畳みに使われたパターンです。展開図は4つの三角形が組み合わさった形になっていて、それぞれが蛇腹折りで折り畳まれます。上の写真のように折った後で、これを中心の四角形に巻きつけます。
※
小型ソーラー電力セイル実証機「IKAROS(イカロス)」のセイル展開の成功について(宇宙航空研究開発機構 プレスリリース)
※
世界初の宇宙ヨット「イカロス」で挑む太陽系大航海時代(JAXA 森 治)[PDFファイル]
紙でこのパターンを平らに折ってから広げると、双曲放物面状の形になることが知られています(中央部にも折り線を入れます)。不思議な形なので、ぜひ一度作ってみることをお勧めします。その一方で、このパターンから作りだされる形状は、数学的には双曲放物面にならない、ということが「Erik D. Demaine, Martin L. Demaine, Vi Hart, Gregory N. Price and Tomohiro Tachi. (Non)existence of Pleated Folds: How Paper Folds Between Creases, 2009」によって示されています。
ねじり折り

紙をひねって折り畳む構造をしていて、完全に折りたたむと平坦になります。紙が互いに重なり合ってループします(重なりにサイクルがあります)。中央部分は正方形である必要はありません。下の写真は中央が三角、四角、六角の例です。畳紙(タトウ)や「花紋折り」などに見られ、またTessellationと呼ばれる分野の折りにもよく登場します。

三角形のスパイラル

三角形の集合で円錐状の形が構成され、平坦に折りたたむことができます。折り畳んだ状態を上から見ると、三角形が中から外に向かってらせん状に広がります。折り紙作家の布施知子氏によって、このパターンを持った作品が多く作られています(※1)。また一方で、野島武敏氏(東京工業大学特任教授)によっても、その設計手法が研究され(※2)、それぞれ「ねじれ多重塔」、「円錐殻」などの名称で呼ばれています。ねじれの角度や重ねる段数を変えることが可能で(上記は5角形の例)、2010年に発表された 132 5. ISSEY MIYAKE シリーズの服飾にも、このパターンのバリエーションが使用されたデザインが含まれます。
※1 布施 知子, MANIFOLD, #05, pp.3–5, 2002.
※2 野島 武敏, 折りたたみ可能な円錐殻の創製, 日本機械学會論文集. C編 66(647), pp. 2463-2469, 2000.
折り紙に関する研究分野
「折り紙の研究」と言っても、折り紙の文化歴史の研究から、幾何学的な観点からの研究まで幅広くあります。ここでは折り紙についてどのような点が研究の対象となっているのか紹介してみます。
折り紙の設計技法
目的の形を1枚の紙を折って作るにはどうすればよいか?という問題を考えます。平坦折り可能な折り紙であれば、ボックスプリーツを用いた設計、サークルパッキングなどと呼ばれる技法が考案されています。特定の条件のもとで、コンピュータによる基本構造の設計が実現されています。立体的な折り紙についても、各種ソフトウェアが開発されています。
剛体折り紙
折り紙を「多角形の剛板がヒンジで連結されたモデル」に置き換えた上で、折りたたむことが可能な構造物の設計を考えます。一般的な折り紙の折り工程には、紙のねじりや曲げが含まれ、剛体折り紙として扱うと折りたためない場合がほとんどです。剛体折り可能な構造は、実際に工業製品や建築物を作る上で重要になります。
曲線折り、曲面折り紙
紙はしなやかに曲げることができるので、曲線・曲面を含む形も表現できます。このような形をした折り紙作品が、Huffman符号で有名な数学者、David Huffman氏によって数多く作られました。一方で、曲線・曲面を含む折り紙の設計技法については限られた範囲でしか明らかにされていません。特に、空間曲線での折りを含む折り紙については、2008年のSIGGRAPHで「Curved Folding」という論文が発表されましたが、その設計方法については、まだほとんど確立されていません。チャレンジの余地がある分野です。
厚みのある折り紙
実際に工業製品に応用するためには、素材の厚さを無視できません。厚さを考慮すると、2次元平面の問題が3次元物体の問題になるため、折りの交差する点での処理に工夫が必要になります。厚みのある素材をきちんと折りたたむ、というのは難しい問題です。
コンピュータ折り紙のインタフェース
私たちが実際に紙を折るときには2本の腕(10本の指)を活用しますが、コンピュータの中で仮想的な紙を折ろうとした場合には、マウスのクリック・ドラッグ操作などで折る必要が生じます。どのようなインタフェースで折るとよいか、どのようなデータ構造がよいかなどを考えます。
ロボットによる折り紙
ロボットのマニピュレータの開発において、その「器用さ」を示すパフォーマンスとして、折り紙をすることがよく行われます。ロボットで紙を折る、ということは難しいテーマです。とくに「鶴」を折ることは難しい部類に入ります。
生物との関係
昆虫が羽化するときには、小さく折りたたまれた羽根が驚くほど大きく広がります。また、植物のツボミが開花する時も同様です。その仕組みを解明するために、折り紙の知識が役立ちます。この「小さくたたんだものを大きく広げる」機構は、宇宙船の太陽電池パネルの開閉などに必要とされます。
計算量の理論
例えば、「折り線が与えられたときに、それを平坦に折りたたむことはできるか否か判定せよ」という問題や「妥当な紙の重なり順を列挙せよ」というような問題が与えられたときに、その解を得るのにどの程度の計算量が必要か。などの研究を行います。
折り紙と数学
非常に広い領域です。前述の「計算量の理論」も含まれますが、それ以外にも折り紙で3次方程式を解く。折り紙で正多角形を折る方法を見つける(10角形まではすべて折れる)。山谷の折り線が平坦に折りたためるための条件を明らかにする、などの理論的な考察を行います。
折り紙と教育
折り紙を用いた教育法について研究します。例えば、鶴の展開図から、直角三角形、角の二等分線と三角形の内心、などの幾何の学習を行うことができます。算数の教材として折り紙を活用する方法が多くの方から提案されています。
平坦折り
折り紙で形を作るとき、その折り操作にはカドとカドをあわせるなどして、ペタンと平らに折りたたむ操作が大半を占めます。立体的な形に仕上がる作品もありますが、その途中の工程では平坦な状態であることがほとんどです。伝承折り紙として有名な兜やヤッコさん、セミは完成形まで平らなままで、鶴も最後に翼を広げるまでの各工程は平らに折りたたみます。このように、紙を平らに折る操作は折り紙の基本的な操作で、これを「平坦折り」と呼びます。
平坦折りでできる折り線は必ず直線になります。そのため、平坦折りした紙の展開図はまっすぐな線分の集合となります。下図は、平坦折りで作られる「小鳥」の完成形とその展開図です。展開図は線分の集合で表されることが確認できます。
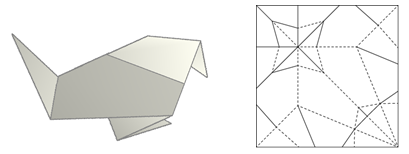
平らに折りたたまれた状態は、折り紙の一般的な状態なので、古くから多くの方が研究の対象としてきました。その成果として、折り線が交差する点に着目すると、次の2つの性質が必ず満たされることが前川定理・川崎定理として知られています。(前川定理の初出については、
上原氏がこちらにまとめています。)
(1)「山折り」と「谷折り」の数の差は±2 (前川定理)
(2) 1つおきの内角の和は 180 度 (
川崎定理)
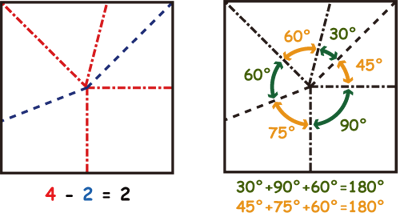
上の図は平坦折りした紙を開いたときに現れる展開図の例で、この2つの定理を満たしています。これ以外にも、さまざまな方法で折り畳んだ紙を実際に開いてみて、2つの定理が常に満たされていることを確認してみましょう。先ほどの小鳥の展開図も、各頂点において、この定理の示す条件を満たしています。
ところで、これらの定理は必要条件であって、十分条件ではありません。つまり平坦に折ることができる展開図は必ずこの条件を満たしますが、この条件を満たすからと言って、必ずしも平坦に折ることができるわけではありません。
局所的な平坦折りに関する必要十分条件については、ここでは詳しく述べませんが「幾何学的な折りアルゴリズム[1] p227」にわかりやすくまとめられています。
ここで「局所的」という言葉を使ったのは、ある1点だけに注目して、その点の近傍で折り畳めるかどうかを議論しているからです。部分的には折ることができても、大局的には(折り紙全体では)紙の衝突が起こって実際には折り畳めない、という展開図も存在します。このような「局所的には折れるけど大局的には折れない」という状況を理解するには、次の単純な展開図を考えるといいでしょう。左側の展開図は、2つの谷折り線を折ると紙がぶつかって平らに折り畳めません。一方、右側の展開図は紙がぶつからないので平らに折りたためます。
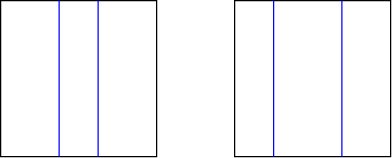
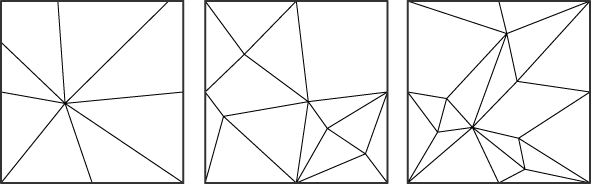
下の図は少し複雑に見えますが、あらゆる点で上記の条件を満たし、なおかつ大局的に折りたたむことができます。是非、実際に折り畳めることを(図を印刷して)確認してみてください。
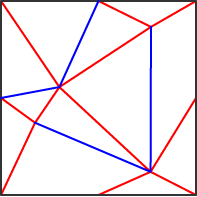
下の図は、平坦折り可能な展開図の山折り、谷折りの区別をなくしたものです。うまく山・谷を割り当てることができると平坦に折り畳むことができます。初めての場合には少し苦戦するでしょうが、経験を積むとすぐにできるようになります。あたえられた展開図が大局的に折りたたまれるか否かの判定はNP困難な問題であることが知られているため※2、「与えられた展開図を折る」というのはちょっとしたパズルとして楽しめます。これらの展開図はコンピュータで自動生成しました。その方法については文献※3にまとめてあります。
※1 Erik D. Demaine, Joseph O’Rourke, 上原 隆平 (翻訳), 幾何的な折りアルゴリズム―リンケージ、折り紙、多面体, 近代科学社, 2009.
※2 M. Berm, B. Hayes. The complexity of flat origami. In Proc. 7th ACM-SIAM Symposium Discrete Algorithms, pp. 175-183, (1996).
※3 Jun Mitani, A Method for Designing Crease Patterns for Flat-Foldable Origami with Numerical Optimization, Journal for Geometry and Graphics, Vol.15, No.2, pp.195-201, (2011).
折りと鏡映変換(平坦折り)
ある図形を鏡に映した形に変換する操作を「鏡映変換」と呼びます。この鏡映変換と折り紙の折り操作は密接な関係を持っています。
まずここでは、平らに折りたたむ平坦折りに限定して「折る」という操作を考えてみます。平坦折りなので、折り線は必ず直線になり、折る操作は180度の角度で折ることになります(折り線を軸にして180度回転させる、つまり「折り返す」ということ)。これはつまり、折り紙を置いた面を上から見下ろすと、紙の一部を折り線によって鏡映変換したことになります。
例えば、下の図のように、折り紙のカドを破線で折り返してみます。すると、折り返す前のカドの形Aと、折り返した後の形A'は鏡映の関係にあります。
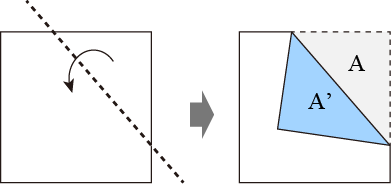
さらにもう一度折ってみましょう。その様子を下図に示します。180度の回転ですので、紙の重なり順が上下逆になりますが、2次元平面でのカタチだけに注目すると、折る前の形Bと折った後の形B'は、やはり鏡映の関係になります。
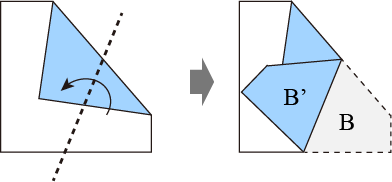
ここまで折った紙を開くと、下図のような展開図が得られます(ここでは山谷の区別をしないものとします)。
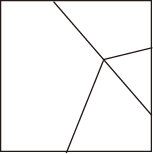
さて、この展開図から、折った後の形を決定することはできるでしょうか。答えは・・・「できる」です。輪郭線と折り線で囲まれた多角形に鏡映変換を施すことで、折った後の形を再現できます(ただし「紙の重なり方」は決定できません)。説明しやすいように、下のように各領域にa〜d、折り線に1〜4の番号を振って説明してみます。
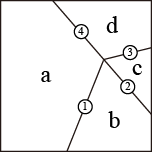
まずaはそのままにして、bを1の線で折り返します。続いて、2で多角形cを折り返します。bが既に反転済みなのでcはそのままにします(反転の反転はそのまま)。さらに続いて、3で多角形dを折り返します。以上で、aを固定した状態で折りたたんだ後のb,c,dの位置が確定しました。折り線4は使っていませんが、折りたたんだ状態で、aとdが折り線4をちょうど共有する配置になります。
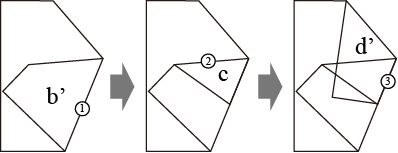
折りたたみ。b', d'は、それぞれb,dの鏡映。
このように、基準となる多角形を固定して、それに折り線を介して接続する多角形を順番に折りたたんでいくことで最終的に折った後の形を求めることができます。折りたたむ順番は任意です。上の例では、aを固定して、b,c,dの順番に折りたたみましたが、これをd,c,bの順番にたたんでも同じ結果になります(繰り返しになりますが、紙の重なり方、つまり多角形の重なり順は、これだけでは決定できません)。
それでは、もう少し具体的な例として、下の展開図を見てみましょう。これは鶴の展開図です。折り紙に詳しい人は、これを見てすぐに「鶴の展開図だ」とわかります。右上が頭、左上と右下が翼、左下が尾(脚?)に対応します。
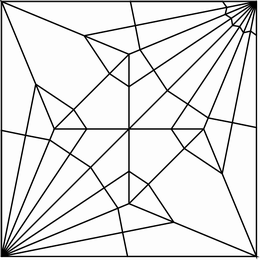
鶴の展開図
上の展開図には、折り線で囲まれた多角形は全部で52個あります。このうちの1つを固定して、隣接する多角形を順番に折りたたみながらたどっていくと、次のような鶴の形が現れます。多角形を辿る順番は自由で、どのように辿っても同じ結果になります。もし、異なる辿り方で異なる結果になってしまったら、それは展開図に誤りがあった(そもそも平らに折りたためない展開図であった)ということになります。
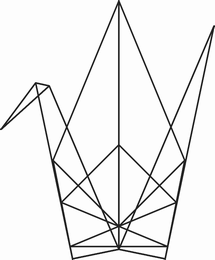
多角形は、1つ辿るたびに180度の角度で折り返す(鏡映変換する)ので、隣り合う2つの多角形は、必ず「一方が元の形のままで、他方が鏡像」ということになります。元の展開図に対して、折りたたんだ後で鏡像となる(裏と表が反転する)多角形に色を付けると次のようになります。白とグレーの多角形が互い違いに並び、決して同じ色の多角形が並ぶことはない、ということを確認できます。このような形の計算はコンピュータで簡単に実現でき、
ORIPAの主な機能の1つになっています。紙の重なり方(多角形の重なり順)の決定方法は、もう少し難しい話になります。
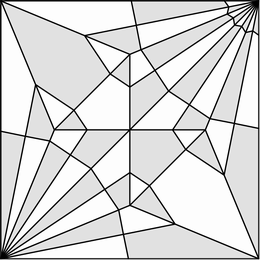
展開図からの紙の重なりの復元
唐突ですが、与えられた展開図から、元の折り紙の形と紙の重なり方を復元することはできるでしょうか。
ここでの紙の重なりとは、展開図に含まれる多角形領域が、折った後に、どのように重なり合うか(各多角形領域の上下関係のこと)を言います。
展開図を折った「形」が復元可能であることは
「折りと鏡映変換(平坦折り)」で述べました。一方で、展開図を折った後の紙の重なり方を決定する問題はNP困難であることが既に示されています(※1)。
つまり、多角形の数の多項式時間で、重なり方を見つけ出すアルゴリズムは存在しないのです。
とはいっても、あらゆる重なり方をしらみつぶしに試せば、展開図の情報と矛盾が無いものを見つけ出すことができるでしょう。では、このアプローチは有効でしょうか。
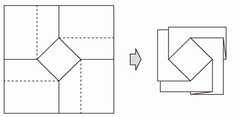
すでに紹介した「ねじり折り(右図)」のように、紙の重なり順にサイクルを持つものもありますから、各領域に1つずつ重なり順を割り振るだけではうまくいきません。互いに重なり合う多角形領域のすべての組み合わせに対して、どちらが上でどちらが下になるのかを割り当てる必要があるのです。
下図の鶴の展開図の場合、多角形領域の数は52なので、多角形領域のペアの数は52x51/2=1326組あります。これらのうち、折った後で一部でも重なる関係にある多角形領域の組は638組あります。したがって、ペア毎にどちらが上になるかで2通りの可能性があるので、全体では2^638通り(約10^192通り)の可能性があることになります。とてもこれを全部調べるわけにはいきません。何か工夫しない限り現実的に解決できない問題であると言えます。

これ以降では、
現在Webで公開されているORIPAに実装されている、紙の重なり方の決定方法を紹介します。ORIPAでは、鶴の展開図に対しても1秒足らずで可能な紙の重なり方をすべて見つけ出すことができます。
重なり決定のアルゴリズム
基本的な考え方を最初に説明しましょう。まず、折り紙全体の問題を局所的な紙の重なり順決定の問題に分割し、局所的に矛盾のない重なり方を選び出します。その後、最終的に全体で矛盾のない重なり方に統合することを行います(この実装方法は、目黒俊幸氏の開発した「オリヒメ」という名称のソフトウェアで実現されていた方法です)。
具体的には、次のような手順で行います。なお、以降では折り線で囲まれた領域のことをface、faceを分割して作られる多角形のことをsubface、折り畳んだ後の位置に応じてsubfaceをまとめたグループをsubfaceGroupと表記することにします。
(1) 展開図を折った後のfaceの位置と向き(表面が上を向いているか下を向いているか)を求める。
(2) faceを複数のsubfaceに分割し、それらをsubfaceGroupにまとめる。
(3) subfaceGroup単位でsubfaceの妥当な重なり順を求める。
(4) すべてのsubfaceGroupで矛盾しない重なり関係を探す。
手順(1)は
「折りと鏡映変換(平坦折り)」で紹介したものと同じですので、以降では手順(2),(3),(4)の内容を説明します。
faceの分割とsubfaceGroupの作成
展開図を折りたたんだ後で、faceをその上を横切る他のfaceの輪郭線で複数のsubfaceに分割します。続いて、同じ位置、同じ形のsubfaceをグループ(subfaceGroup)にまとめます。下図の例ではF1が4つに分割され、F2,F4は2つに分割されます。F3は分割されません。分割されてできたsubfaceは4つのsubfaceGroup(図中のA〜D)にグループ化されます。このグループ単位で妥当な重なり順を求め、その後に全体で矛盾のない重なりを求めることになります。
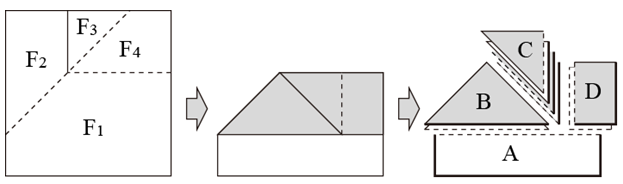
subfaceGroup内での妥当な重なり順
subfaceGroup内で、subfaceを問題なく重ねられる方法を全て調べあげます。上の図で示したように、subfaceGroup内では、同じ形のsubfaceが重なっているため、その境界に着目し、重なり順として適切でないものを除外します。次の図は1つのsubfaceGroupの輪郭に着目した時の断面図で、これに含まれるsubfaceの輪郭線(図中の黒丸)は次の3通りに分類できます。
- E_boundary: 紙の輪郭と一致する稜線
- E_fold_{upper, lower}: 折り線と一致する稜線で、必ず2つ1組で存在します。面の向き(上を向いているか下を向いているか)および折り線の山谷の違いによって上に配置されるものE_fold_upperと下に配置されるものE_fold_lowerを区別できます。
- E_connect:faceを分割することで生成された、折り線ではない稜線。隣接するsubfaceGroupと共有されます。
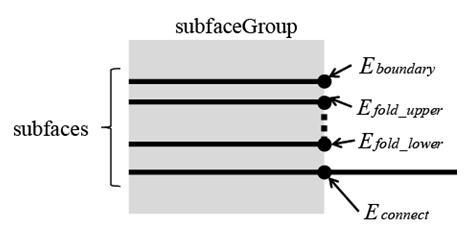
さて、subfaceGroup内に含まれるsubfaceを順番に重ねていった場合、適切でない重なりかたがあります。これには下図に示す3通りのパターンがあります。
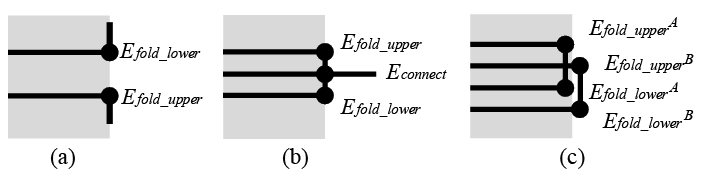
図の(a)が発生するのは、折り線の種類から決定される上下関係に反する場合です。(b)のケースでは互いに接続するE_fold_lowerとE_fold_upperの間を他の面が横切って、紙が交差してしまいます。(c)はEfold_lowerとEfold_upperのペアが複数存在し、それらが互い違いになっている場合で、やはり紙が交差してしまいます。これらのケースが含まれる重なり順は誤りなので、各subfaceGroup単位で、これらのケースがまったく含まれない重なり順だけを、そのsubfaceGroupにおける妥当な解として保持しておきます。
すべてのsubaceGroupで矛盾しない重なり方の構築
続いて、各subfaceGroupで得られた重なり順が、全体で矛盾しない重なり方を求めます。たとえば、下図のようにsubfaceGroup(A)ではFiがFjよりも上に配置されているのに、subfaceGroup(B)ではFiがFjよりも下に配置されているような場合、必ずどこかで紙の交差が起きてしまうはずなので、これは不適切なケースとして除外します。
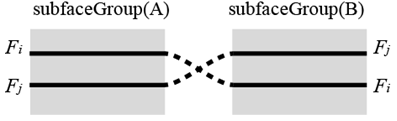
こうして最後まで残ったものが、実現可能な重なり方です。1つの展開図にも、複数の妥当な重なり方が存在します。
展開図から折りたたみ後のかたちの復元例
たとえば下の図は、この方法で兜の展開図から妥当な紙の重なり方をすべて列挙した様子を表しています。右下に通常の折り方で得られる兜の例がありますが、これを含めて9通りの方法が、同じ展開図から復元されうることを確認できます。これらの解は、ORIPAによって発見されたものです。
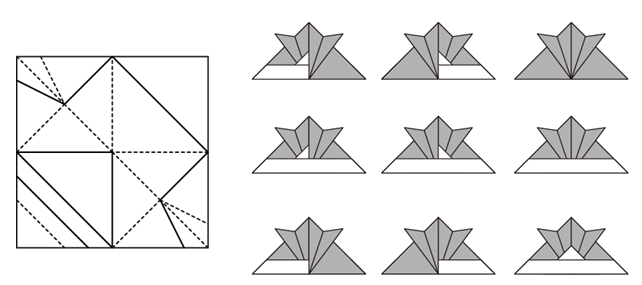
さらに、鶴の場合でも下図のように尾の付け根の一部が外側に出ている場合には、紙の異なる重なり方が存在し、同じ展開図から全部で5通りの方法が復元可能です。これも、ORIPAによって発見されたものです。
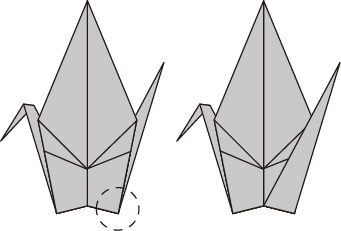
ちなみに、下の「ブタ」の場合は、全部で48通りもの復元方法がありました。
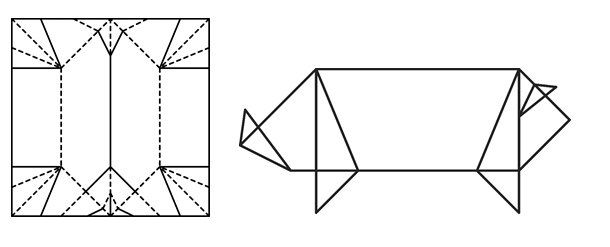
そして、下の「平織り」のパターンの復元方法はただ1つだけでした。誰が折っても、唯一の折り方しか存在しないわけです。コンピュータを使って調べると、意外な面白い発見があります。
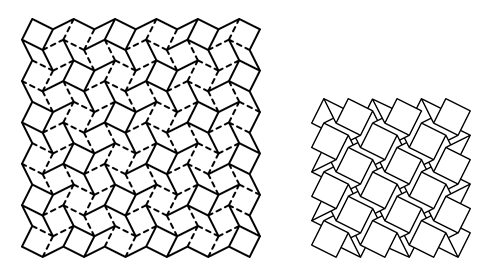
平織り(Tessellation)
紙を折ることで生まれる幾何学的な造形を楽しむ分野の一つに、平織り(Origami Tessellation)と呼ばれるものがあります。
下の図の例のように、平織りには幾何学的な基本パターンを並べることで平面を充填させる特徴があります。

モザイク模様のように見え、光を透かせて陰影を楽しむこともできます。
このような折り技法は服飾に用いられるプリーツにも見られ、古くから多くのパターンが知られています。
近年ではコンピュータを用いたパターン設計も可能となり、新しい折り模様が今も多くの愛好家によって創作されています。
平織りは全体の折り線が互いにリンクしていて、折るときには全体を一度に折る必要があります。
そのため綺麗に仕上げるには手間がかかりますが、できたときの喜びはその分大きなものです。
図を見るだけでは完成形をイメージするのが難しいでしょうから、是非実際に手を動かして折ってみましょう。
正方形を基本としたねじり折り
平織りと呼ばれるものの多くは
「よく知られている折りのパターン」で紹介した「ねじり折り」を構成要素とし、平坦に折りたたまれます。ここではまず、ねじり折りについてより深く見ていきましょう。
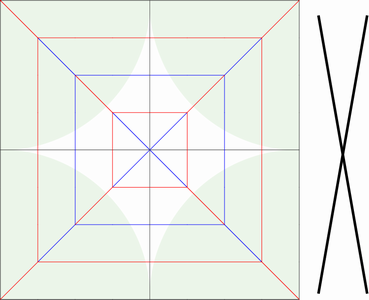
正方形をベースとしたねじり折りは、下図に示すような折り線から構成され、一般的な折紙用紙から簡単に折り出すことができます。
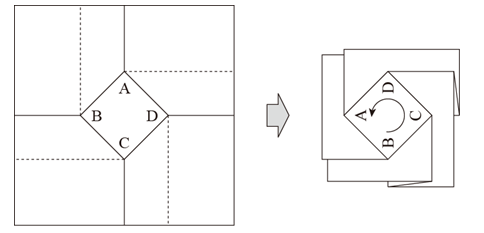
展開図を見ると、45度傾いた正方形が中央に置かれ、水平、垂直方向に折り線が伸びています。これを折りたたむと、中央の正方形が反時計回りに90度回転します。紙をねじるようにして折りたためるのでねじり折りと呼びます。
鏡像パターンの連結
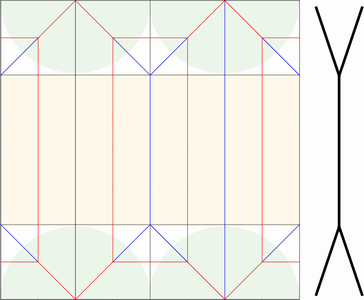
正方形を基本としたねじり折りは、一方を鏡映反転することで下図のように連結できます。
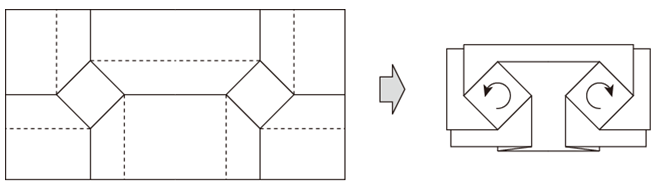
この連結したパターンは互いに干渉することなく、整合性を保ったまま折りたたむことができます。互いに連動するので、実際に折るときには、両方をいっぺんに動かすようにします。一方は他方の鏡像なので、ねじる方向は逆になります。
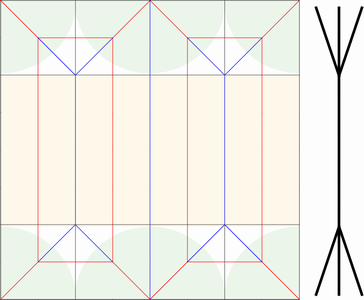
さらに、このパターンを水平線で鏡映反転して連結すると下図のようになります。中央部に大きな閉領域ができますが、これも問題なく折りたためます。
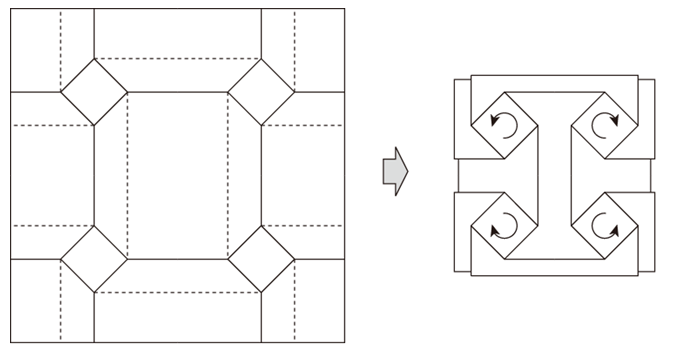
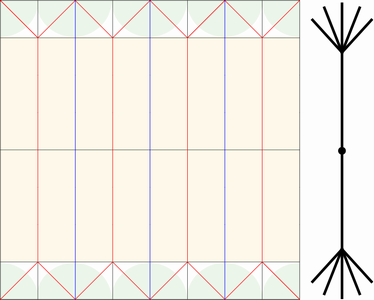
以上のような観察結果から、正方形を基本とするねじり折りは下図に示すようにいくつでも連結でき、平面上に敷き詰められることがわかります。
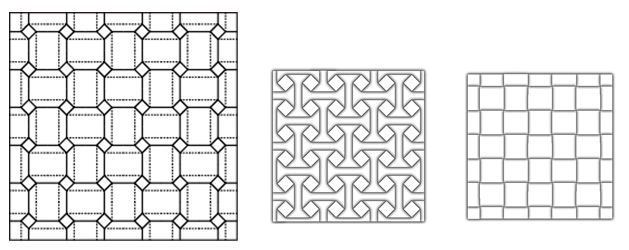
左から展開図、表面、裏面。実際に折った後は、展開図に比べると小さくなる。
互いに隣接するねじり折りは、一方が他方の鏡像になります。これが平織りの1つの例になります。中央部の正方形の大きさの比率を変えることで、異なる印象の平織りを作り出すことができます。
山谷反転パターンの連結
先ほどの例では、鏡映反転を使って隣り合うねじり折りのパターンを連結していましたが、下図のように折り線の位置はそのままにして、平行移動させて連結することもできます。その際に、山谷の符号を反転させます。一方の正方形は裏側に現れることになります。
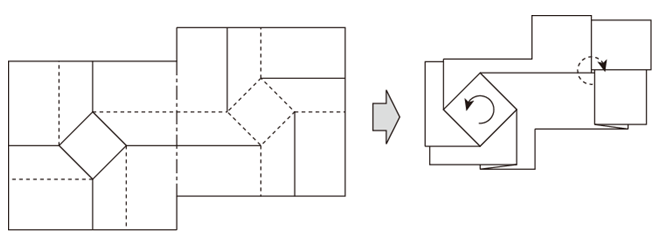
このようなパターンもやはり連結を繰り返して平面を充填できます。4つ連結させると次のようになります。「鏡像パターンの連結」とは異なり、裏と表は区別なく同じになります。
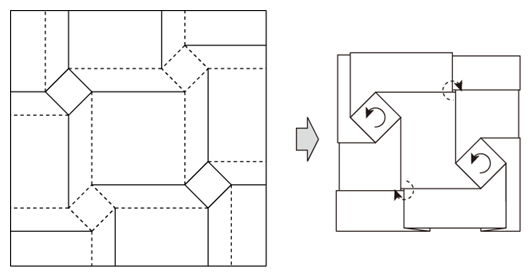
正方形のねじり折りを基本としたパターンのバリエーション
これまでに見てきた「ねじり折り」は平坦に折りたためますが、なぜ折りたためるかを改めて考察してみましょう。
「
平坦折り」で紹介したように、平坦に折りたたまれる展開図の頂点に注目すると、1つおきの内角の和が180度であるという法則(川崎定理)があります。改めて下の図を見てみると、正方形の内部から反時計回りに90度、45度、90度、135度であり、確かにこの法則が成り立つことが分かります。

基本となる中央の多角形が正方形なので最初の90度は固定です。すると、それと対を成す角も90度で固定となります。残りの角に注目すると、これは45度と135度に限定されないことがわかります。一方をθとすると、他方は180°-θとなり、θの値は自由に設定できます。
例として、正方形の傾きを変えてθを20度にしたパターンは下図のようになります(折った後の図は隠れて見えない折り線も表示しています)。角度を小さくすると、重なる領域が小さくなり、裏側には正方形の隙間が生まれることになります。
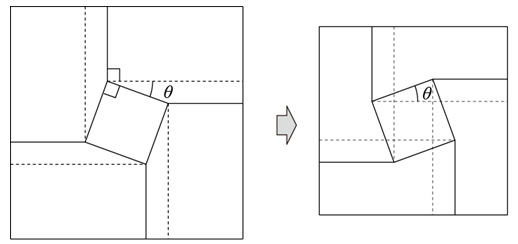
傾きの角度を変えたねじり折りのパターンも、これまでの例と同様の方法で連結し、平面上に敷き詰められます。このバリエーションは、基本となる正方形の大きさと、回転させる角度θの値という2つのパラメータで形を決定できます。
傾きを変えたねじり折りに、「鏡像パターンの連結」を適用すると、折った後の裏側はとても興味深い外観になります。
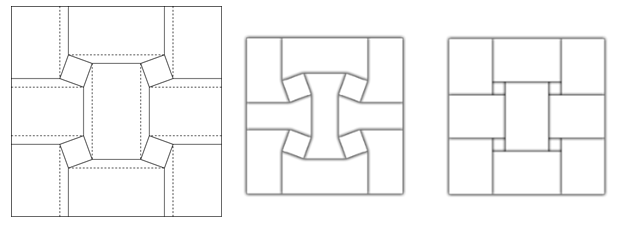
複数の基本パターンを連結すると、下図に示すように、1枚の紙を折っただけでありながら、まるで複数の帯が互い違いに交差した織物(文字通り「平織り」の外観)のように見えます。
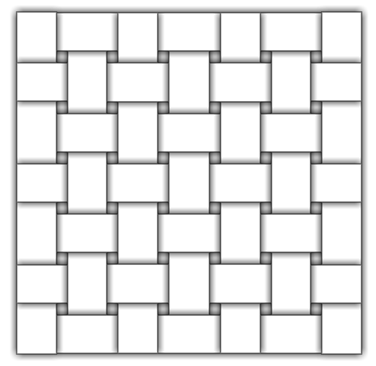
正三角形、正六角形をベースとしたねじり折りのバリエーション
正方形のねじり折りだけでも、いろいろなバリエーションを作れることを確認しましたが、平面を敷き詰められる正多角形には、ほかにも正三角形と正六角形があります。そのため、下図に示すねじり折りも、これまでと同様にして平面を充填することができます。
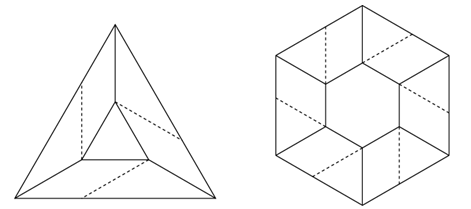
正三角形と正六角形、それぞれを敷き詰めたタイリングパターンは双対の関係(各タイルの中心を連結して作られるパターンが他方と同じものになるという関係)を持つため、上の基本パターンを敷き詰めて得られるものは結果としてどちらも下図に示すものになります。よく見ると、正三角形のねじり折りと正六角形のねじり折りが混在していることがわかります。
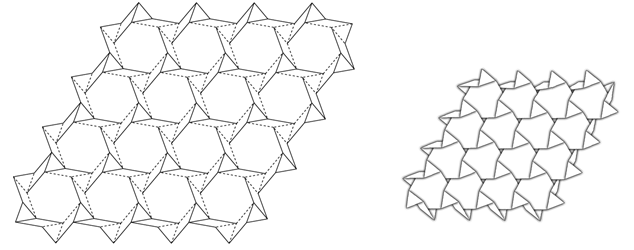
正三角形を平面に敷き詰めると1つの頂点に6つのタイルが接続するので、山谷の反転または鏡映のパターンを交互に配置できます。一方で、正六角形の場合は1つの頂点に3つのタイルが接続するので、山谷反転または鏡映のパターンを交互に配置できず、基本パターンとは異なる山谷の付け方で折りたたむことになります。
異なる正多角形によるタイリング
これまでは、同一の多角形を敷き詰めて作るパターン(正平面充填形と呼びます)に基づく平織りを見てきました。それでは、異なる正多角形の組み合わせによる平面充填のパターン(Uniform Tiling)からも平織りを作り出せるでしょうか。
この問いに対する回答はYESです。異なる正多角形を敷き詰めてできるタイリングについても、下図に示す「縮小して回転させる」という手順で、平らに折りたたまれる展開図を作れることが知られています[1]。
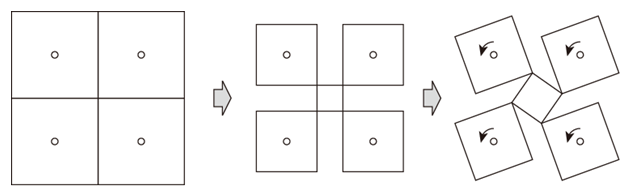
まず、平面に敷き詰めた各正多角形を、その重心を中心として同じ比率で縮小します。すると隙間ができるので、もともと同じ場所にあった頂点同士を連結して、新しい多角形を作ります(同じ場所にあった頂点が4つの場合は四角形が作られます)。
続いて、縮小した多角形を一定角度だけ回転させます(新しく作った多角形もそれに合わせて回転します)。不思議に感じられますが、このようにして作られたパターンは、各頂点が局所平坦折り条件を満たすので、平坦に折りたたむことができます。
このようなアプローチで平織りの展開図を生成できるソフトウェアがAlex Batemanによって開発され、
「Tess」という名称でインターネット上で公開されています。
正多角形の組み合わせで平面を充填するタイリングパターンの中で、すべての頂点の形状が一様なパターン(アルキメデスの平面充填と呼ばれます)は正平面充填形を含めれば全部で11種類ありますが、頂点の形状が一様でなくてもよいのであれば、それらは無数にあります。したがって、この「縮小して回転させる」という驚くほど簡単な操作で、無数の平織りパターンを生成できるのです。下図は「Tess」によって、正八角形と正方形の組み合わせによるパターンを生成した様子です。
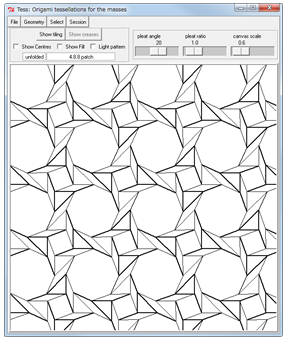
では、この「縮小して回転させる」という操作で平織りパターンを作る方法は、正多角形のタイリングだけに有効なのでしょうか。いえ、この操作は非常に強力で、「隣接する2つのタイルの回転中心を結ぶ線と、2つのタイルが接する辺の成す角が90度である」という条件を満たせば、どのような形のタイルの組み合わせでも実現可能なことがLangらによって示されています[2]。
無限に広い平面を充填するには、何かしらの周期性が必要になりますが、ボロノイ図はこのような条件を満たしますので、下図に示すようなランダムな点群によって生成したボロノイ図からも、「縮小して回転させる」という操作で平坦に折りたためる折り線を生成できます(ボロノイ図から平織りを行う試みは過去に
Eric Gjerdeによって試みられています)。

ランダムな点群から生成したボロノイ図(左上)、各多角形を30%縮小させて20度回転させて作った展開図(右上)、展開図を折りたたんだ様子(下)
立体的な基本要素の配置
これまでは平らに折りたたまれるものに限った話をしてきましたが、さらに対象を広げて立体的な折り構造のタイリングについて考えてみましょう(海外ではOrigami Corrugationsと呼ばれることもあります)。
筆者の開発した
ORI-REVOというソフトウェアで作られる折り紙の形の1つに、下図に示すような、多面体の外側に三角錐状の突起がついたものがあります。
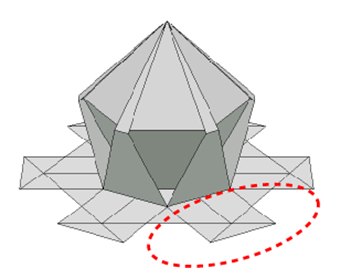
この形状は展開図および折った後の底面が正多角形になるので、やはり平面上に敷き詰めることができます。図中の丸で囲った部分の幅を隣接する構造体と一致させることで、異なる立体形状を連結させることも可能です。
正多角形から構成されるタイリングパターンに対しては、このような立体構造を配置できることになります。
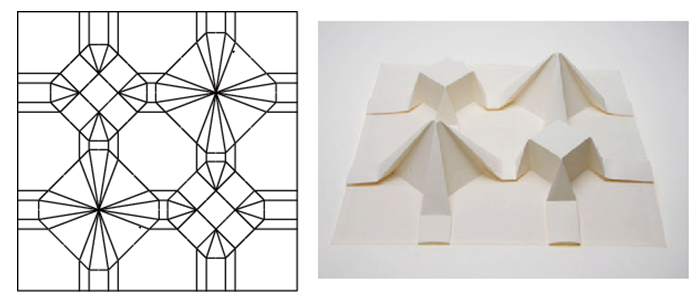
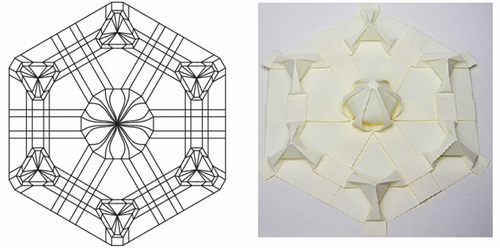
他にも、下図に示すような立体構造を持つ要素を平面上に並べることができます。理論上はいくつでも連結できますが、実際に紙を折る工程では全体を一度に仕上げる必要があるため、あまり数が多いものを作るのは困難です。

さまざまな平織り
これまでに、周期的な折りのパターンで幾何学的な造形を作り出す平織りについて紹介しました。ねじり折りを組み合わせて作るパターンには際限がなくさまざまなものがあること、そして立体的な折り構造をもつ形も組みあわせられることを紹介しました。もちろん、ねじり折り以外の折りを組み合わせることも可能です。多くの折り紙作家による、装飾の美しい作品がインターネット上には多数公開されています。たとえば
Flickr上のOrigami Tessellationsのグループには、執筆時現在1060のユーザが登録されていて、変化に富んだ数々の作品の写真を見ることができます。平織りは、紙による造形のとても興味深い分野の1つです。
[1] アレックス・ベイトマン, 平織り(折り紙テッサレーション)デザインのためのコンピュータ・ツールとアルゴリズム, 折り紙の数理と科学, Thomas Hull編, 森川出版. 第12章 (2005)
[2] Robert J. Lang, Alex Bateman, Every Spider Web Has a Simple Flat Twist Tessellation, Origami5, CRC Press, pp.455-473 (2011)
ジャバラ折り展開図の見方・作り方
下図のような格子模様の上に折り線を付けて紙を畳む方法を蛇腹(ジャバラ)折りと呼びます。

「よく知られている折りのパターン」の節で紹介した多くの展開図が、この格子模様から作り出せます。
格子状に配置された折り線を折りたたむときに、山と谷を交互に折ることが多いので、蛇腹(ジャバラ)折りと呼ばれますが、矩形の襞が折り出されることから、「ボックスプリーツ(box pleat)」とも呼ばれます。
格子模様は正方形の紙から簡単に折り出すことができ、バリエーションに富んだ形をさまざまに生み出すことができます。
上の例では、各辺を8等分していますが、たとえば16等分、32等分と細かくすることで、さらにバリエーションは増えます。
昆虫やリアルな人物モデルなど、従来の折り紙の概念を覆すような複雑で精巧な折り紙作品が数多く登場していますが、その多くが、この格子模様をベースに作り出されています。
一見すると、直線ばかりのカタチしか作れないように見えますが、まずは目的の基本構造を持った形を作り出し、そこからディテールを追加して作品を仕上げるのが一般的です。
例えば、イヌのように、足が4本、しっぽと頭部があるカタチを折り出そうとしたときに、まず、その基本的な構造を折り出すことを考えて、それから細かいところの作りこみを行います。コンピュータを使った折り紙の設計技法もありますが、紙と鉛筆、それと実際の紙を使っての創作においては、この格子模様を使うことがとても便利で、精巧な折り紙を実現するための設計技法の1つとして、現在広く使われています。
それでは、具体的な展開図の例を見てみましょう。
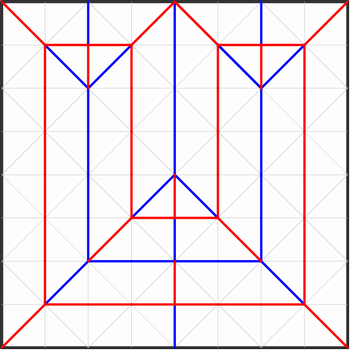
一般的な展開図は上のようになります。これを見て、折った後にどのような形が得られるか(どのような構造になっているか)すぐにわかるでしょうか。おそらく、すぐにわかる人は少ないと思います(その説明のために、この文章を作っています)。
しかしながら、ジャバラ折りを使った折り紙の創作を行う人たちの間では、このような展開図を見れば構造がすぐわかり、新しい折り紙作品の作り方も、このような展開図で記録しておくことがふつうです(もっとシンプルに、展開図の一部分だけを記録することも多いです)。
上の例は、高々8x8の格子模様から作られるパターンですが、作品によっては32x32さらには64x64の格子模様が使われます。一般に、ジャバラ折りの場合は1つ1つの折り工程があるわけではなく、展開図に沿って「いっぺんに折る」または「好きなところから折る」ということが多いので、折りの工程図を示さずに、展開図だけ示して終わりなことが多いです。そのため、通常の折り紙の本に載っている手順に従って、一工程ずつ紙を折り進めることがメインの人たちから見ると、ジャバラ折りを駆使した複雑な折り紙の世界は理解が難しい別世界のもののように見えてしまいます。
さて、ためしに一度、「折り紙 ジャバラ 展開図」をキーワードとした
画像検索をしてみてください。一般の人にはまったく理解できない図が大量に見つかると思います。しかし、このような図があれば、目的の構造を持った折り紙作品を再現できるのです。つまり、新しい折り紙作品の設計は、このような図を書くことで実現することもできるのです。
というわけで、上の展開図についても折り工程を示す図はありません。展開図が示す通り、赤線を山、青線を谷に折ってみましょう。
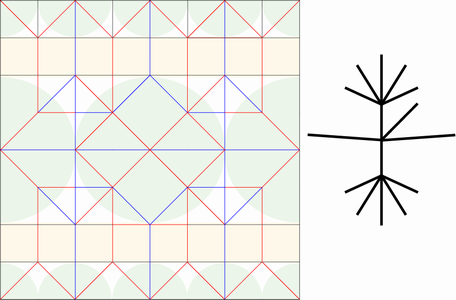
その結果、次のように棒状に折りたためます(広がらないように両端をクリップで留めています)。今回の展開図は、折りたたまれて平らになり、その際に紙の輪郭線が見事に1本の直線の上に乗ります。紙の輪郭線は太い線にしてあります。

上の写真、見た目は面白くないですが、一般的なジャバラ折りは、このように棒状に折りたたむことを行います。これを開くと・・。
次のような形になります。手足がついた、人間のカタチのようにも見えます。

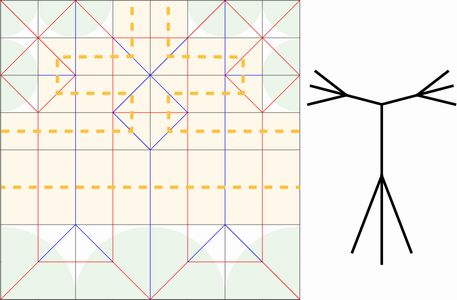
つまり、格子模様の上に、適切に山・谷の折り線を配置すると、次のような構造を作り出すことができる。ということです。
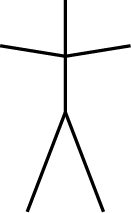
正方形の紙のカドは4つしかありませんが、胴体と5本の枝を持つ構造が作れています。このような、任意の本数の枝を持つ構造を意図して作り出すことができれば、後から全体を少し開いたり細かい部分を追加したりして、形を作りこむことができます。

それでは、改めて、展開図と折った後に現れる棒状の構造(木構造、Stck Figure、骨格構造などと呼ばれます)の関係を見てみましょう。以降では Stck Figure と呼ぶこととします。わかりやすくするために、色を付けました。
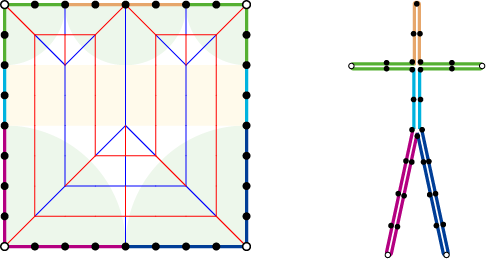
折られた後の紙の輪郭線は、右側の Stick Figure を形作ります。輪郭線とStick Figureの対応関係は、色で確認できます。じっくり見てみましょう。輪郭線の左下隅(紫)と右下隅(紺)は、それぞれ Stick Figure の左下と右下に対応します。展開図の左右に分かれている水色は、Stick Figureでは、合わさって胴体部分になっています。展開図の左上と右上(緑)は、Stick Figureの左右の腕に対応し、展開図の上部中央(オレンジ)はStick Figureの頭部に対応します。
正方形の輪郭を見ると、1辺あたり8個の線分があり、全体で8x4=32個の線分があります。同じように、Stick Figure の線分の数をかぞえてみると、やはり32個あります。紙の輪郭線で、Stick Figure を構成し、紙の内部は蛇腹状に折りたたまれていることがわかります。
さて、紙の輪郭線とStick Figureの対応はわかりました。それでは、紙の内部はどのようにして折りたたまれているのでしょうか。これは、展開図を四角形の部品に分解してみるとわかります。
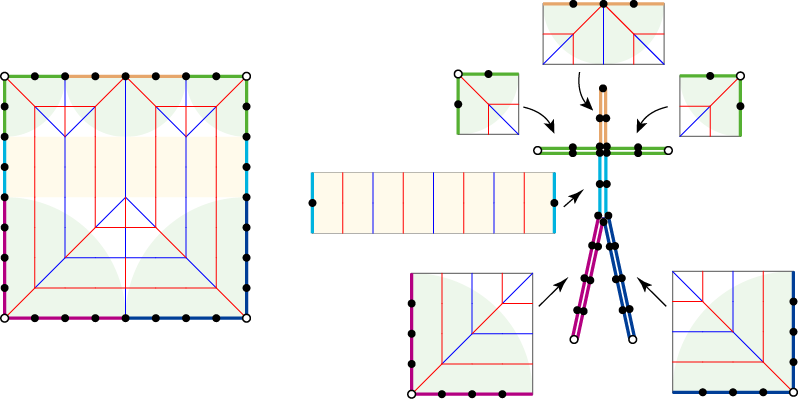
Stick Figureの水色の部分は幅が2の単純なジャバラ折りであることがわかります。このように、Stick Figureの枝と枝をつなげる辺は、帯状の部品を折りたたんで作られます。
それ以外の、Stick Figureの枝は、それぞれの長さに応じた四角形領域で作り出されます。左下と右下は1辺が4の正方形領域で長さ4の枝が作り出されています。ほぼ同じように、左上と右上は、1辺が2の正方形領域で長さ2の枝が作り出されています。
中央上部は、4隅と異なり、縦2横4の長方形から作り出されます。このように、「4隅でないところからも枝を作り出せる」という点が重要です。つまり、広い紙があれば、いくらでも枝(「カド」と表記することも多いです)を作り出すことができるのです。
各部品の背景に薄緑色の円が示されていますが、これは「円の半径と等しい長さの枝を折り出せる」ということと、「円の中心が枝の先端になる」ということを示しています。
さて、1つの展開図を複数の部品に分解することで、Stick Figureと展開図の対応関係が見えてきました。これを逆に見ると、複数の部品を組み合わせることで、目的の構造を持ったStick Figureを1枚の紙から折り出すことができそうだ。と考えられます。
それでは、「部品」にはどのようなものがあるでしょうか。
一番単純な、紙の4隅から枝部分を折り出すには、次の部品が使えます。それぞれ平らに折りたたむことができ、折りたたむと左から順番に長さが4, 2, 1の枝になります。
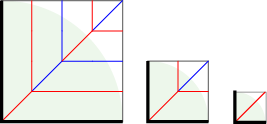
紙の辺から枝部分を折り出すには、次の部品が使えます。それぞれ平らに折りたたむことができ、折りたたむと左から順番に長さが4, 2, 1の枝になります。
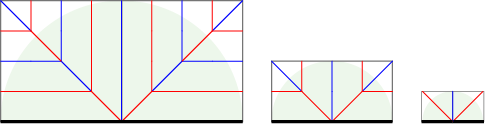
さらに、紙の中央部でも次のような部品を使って、枝を折り出すことができます。ただし上記の4隅、辺から折り出す例と異なり、そのままでは棒状の細い平らな状態に折りたためないので、周囲の部品との兼ね合いで、山谷を決めることになります。左から順番に長さが4, 2, 1の枝になります。
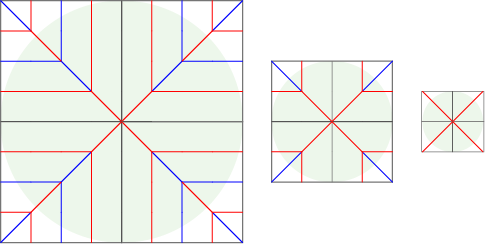
枝と枝をつなげる辺の部分は、すでに見たように、幅が一定の単純なジャバラで折り出すことができます。下の図は、上が幅2、中央が幅1のジャバラです。また、不思議に見えますが、一番下のように、幅が一定であれば折れ曲がった領域からも、辺の部分を折り出すことができます(試しに一番下の例を折ってみましょう。平らに折った後で、紙の縁にあたる部分が一致します)。
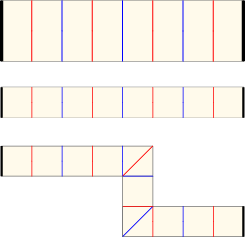
ところで、枝が分岐する点では、枝は自由な方向に曲げられます。これまでに見てきた、人の骨格構造の例で言うと、腕の付け根の関節は自由に動いて、腕を開いたり閉じたりできます。つまり、骨格構造として見た時には、腕の付け根の折れ線は山折りなのか、谷折りなのか、または折らない線なのかを明示する必要が無いと言えます。例えば、下図の例のように各分岐点を開いた状態にした場合、山折りと谷折りが明確に定まりません(完全に平らに折りたたんでしまえば、山と谷は定まります)。このような、自由に回転できる折り線を「ヒンジ」と呼び、展開図では山と谷を明示しないことがあります。下図では、ヒンジに該当する線をグレーで示しています。ちょうど各部品の境目がヒンジになり、部品の配置が視覚的にも理解しやすくなります。一方で、実際に折るときには山と谷のどちらにすればよいのか、試行錯誤が必要になります。
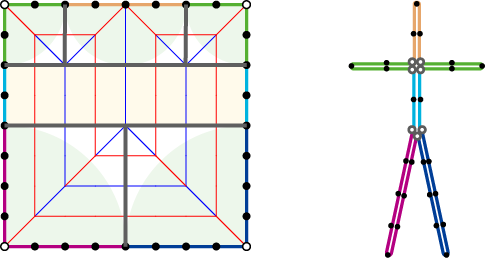
さて、以上で、ジャバラ折りを構成する部品を見てきました。実際の創作には、もっと多くの知識と経験が必要になりますが、格子模様から作り出される部品を組み合わせることで、さまざまな骨格構造を折り出すことができることを理解できたことと思います。
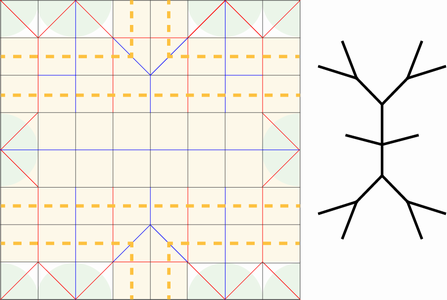
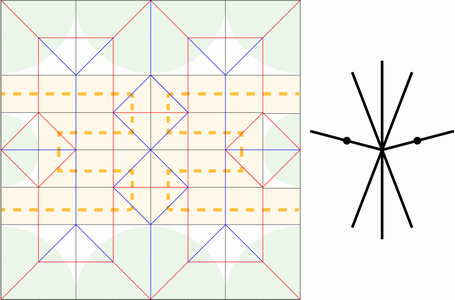
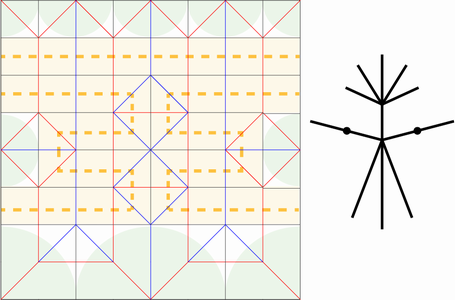
8x8格子パターンからできる構造
1枚の紙で表現可能な曲面
紙は基本的に伸縮しない素材ですが、しなやかに曲げることができます。1枚の紙で表現できる曲面は「可展面」(または可展面の集合)に限られることが知られています。可展面とは、「線織面」と呼ばれる直線エレメントの集合で表現される曲面集合の中の一部です。可展面には、「柱面」、「錐面」、「接線曲面」の3種類があり、それぞれ直線エレメントが「平行」、「1点で交わる」、「空間曲線に接する」という特徴があります。
文章で説明するのはなかなか難しいですね。そこで、線織面の分類を図で表すと次のようになります。
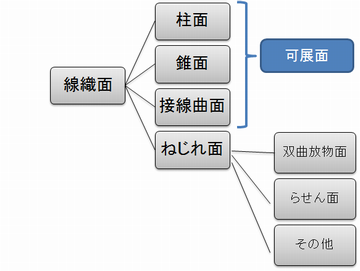
具体的な図を使って示すと次のような感じになります。一番左側の曲面は双曲放物面と呼ばれる曲面です(数ある線織面の中の一例にすぎません)。
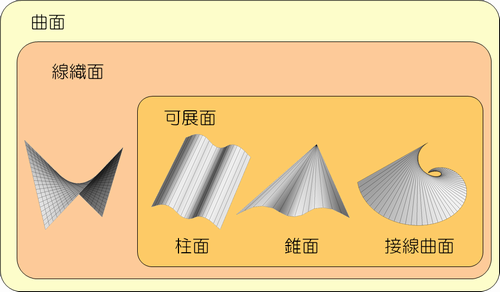
このように可展面にはいくつか種類がありますが、直線エレメントが平行な柱面は、正方形(または長方形)の紙で簡単に作れるので扱いやすい曲面であると言えます。
ORI-REVOで設計される折り紙の形は、直線エレメントがすべて平行なので、柱面の集合で構成される形です。例えば下の例は、球体を包むような形に仕上がっていますが、構成面はすべて柱面で、展開図は長方形の形になります。

折りと鏡映変換(立体的な折り)
平坦折りでの折り操作が、2次元図形の鏡映変換に相当することをこれまでに述べてきました。
折った後の形が立体的になる折り紙でも、折り線が平面に乗るような折り操作であれば、それを鏡映変換で表すことができます。下の図を見てみましょう。左側は、山折り線と谷折り線が交互に並ぶ「蛇腹折り」です。この中央付近を平面で切断し、切断された一方をこの平面で鏡映変換すると中央で示すようになります。この操作を上から眺めた様子が右側になります。このような操作を行った形は、やはり1枚の紙で作ることができます。
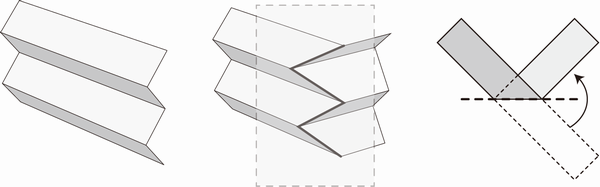
鏡映変換で折り操作を表現できるのは蛇腹折りに限りません。下図のように、曲面でも構いません。立体の一部を鏡映変換すると、鏡映変換された箇所の山谷が逆転し、展開図には新しい折り線が追加されることになりますが、それ以外の影響はありません。元の形が1枚の紙で作れるのであれば、あとの形も、やはり1枚の紙で作れます。
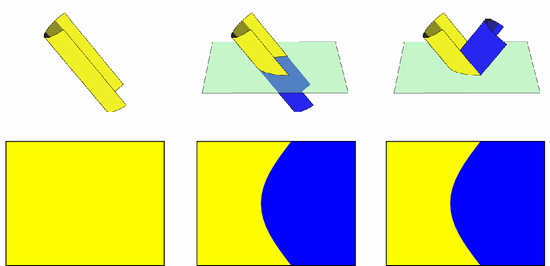
円錐は可展面で、1枚の紙を丸めて作れるので、たとえば下図のように円錐を平面で切断し、一方を鏡映反転する、という処理を繰り返すことで、複数の「曲線の折り」を含む形を作り出すことができます。

次の例は、このようなアプローチで設計された作品です。
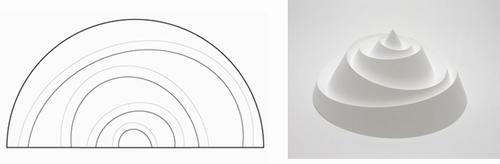
ハフマン符号の考案者として有名な数学者David Huffman氏も、このような円錐の鏡映反転を使った折り紙作品を多数制作しています。
私の開発した
ORI-REFは、このようなアプローチで立体的な折り紙を設計するソフトウェアです。入力として可展面を与えると、あとは鏡映変換の繰り返しで複雑な形を作ることができます。一般に、平面を意図した角度で意図した場所に素早く配置するのは難しいので、鏡映面の存在を意識しないで、マウスのドラッグだけで簡単に操作できる点がORI-REFの特徴です。このソフトウェアを使って、次のような形を作ることができます。

一般に、紙は空間曲線で折ることもできますが、この鏡映変換で得られる折り線は、平面曲線に限定されます。
「空間曲線で折る」ということをシミュレートし、かつ、意図した形を設計できるようにすることは、まだ難しい課題です。
折り紙用ソフトウェア
折り紙の設計技法の確立とコンピュータの普及により、新しい折り紙の創作を支援するソフトウェアが多く開発されるようになりました。そのいくつかはインターネット上に公開され、自由に使えるようになっています。ここでは私が知っている範囲でそれらの紹介を行います。いずれも、ソフトウェアが公開されているWebページや、ソフトウェアに付属するマニュアルに詳細な説明が付属するので、詳しくはそちらをご覧ください。
TreeMaker (Robert J. Lang, 1990年代の初め)
※
TreeMakerのWebページ
Circle-river packing と呼ばれる設計手法に基づいて展開図を自動生成するプログラムです。目的の構造を線分の集合(木構造)として入力とすると、その構造を1枚の紙で折りだすための展開図が自動生成されます。目的の構造には、接続関係とともに長さ情報も含めることができます。昆虫のように分岐の多い複雑な構造をもった対象を折り出すのに役立ちます。用いている設計手法に依り、出力される展開図はuniaxial baseと呼ばれる基本形になります。これは平坦に折り畳むことが可能で、平坦にした状態ではすべてのカドが共通する1つの直線上に並びます。得られた基本形状に対して、細部を作りこむことで折り紙作品を完成させます。開発者であるRobert J. Lang氏は、実際にこのソフトウェアを使って極めて精巧な昆虫の折り紙作品を創り出しました。
ReferenceFinder (Robert J. Lang, 1990年代後半)
※
ReferenceFinderのWebページ
数学的なアプローチで折り紙の設計を行うと、例えば「点(0.21, 0.73)と点(0.52, 0.32)の2点を結ぶ線で折る」というように数値で折り線が表現されるため、実際に折るときには定規を使って点の座標を求める必要が生じます。これでは「道具が無いと折れない」ということになってしまいます。このような問題を解決するためには、任意の点を「折り操作」だけで求める必要があります。この支援を行うのがReferenceFinderです。座標値を指定すると、その点を許容誤差内で折り出すための手順を自動で求めることができます。
Robert J. Lang氏は、上記のソフトウェアのほかにも、平坦折りの操作をシミュレートする
「Origami Simulation」も公開しています。
Tess (Alex Bateman, 2000年前後)
※
TessのWebページ
Paper Mosaic、Origami Tessellation、平織り、など呼ばれる、幾何学的な折りのパターンを生成するソフトウェアです。アルキメデスのタイリングなどの基本的なタイリングをベースに、各頂点をねじり折りした平坦折り可能なパターンを生成します。光に透かして、規則的な陰影のパターンを楽しむことができます。下の図は、Tessで生成したパターンと、それを折った様子です。全体が連動するため、端から順番に少しずつ折って仕上げる、ということができません。全体を一度に折りあげる必要があり、実際に折るのはなかなか大変です。

Rigid Origami Simulator(舘 知宏, 2007)
※
Rigid Origami SimulatorのWebページ
入力として与えられた展開図を剛体折りする様子をアニメーションで表示するソフトウェアです。入力とする展開図は山・谷の区別がついていて、剛体折り可能であることが前提となります。実際に紙を折る前に、どのように変形するかを視覚的に確認することができます。
Origamizer (舘 知宏, 2008)
※
OrigamizerのWebページ
円板と同相の多面体モデルを1枚の紙で折るための展開図を自動生成します。三角形の集合で表現された対象形状に対し、それぞれの三角形を平面上にバラバラに配置し、その隙間にヒダを割り当てます。三角形の適切な配置とヒダのサイズを計算で求めています。ヒダは立体の内側に折り込まれ、外からは見えなくなります。CGの世界で有名なStanford Bunnyを1枚の紙で折ることに成功し、さまざまな形を1枚の紙で表現できることが示されました。
Freeform Origami (舘 知宏, 2010)
※
OrigamizerのWebページ
「平坦折り可能」という条件と「剛体折り可能」という条件を満たしながら、展開図と折った後の形を同時に編集できるソフトウェアです。「平坦折り可能」と「剛体折り可能」という条件はどちらも非常に厳しく、この条件を満たす形を手作業で設計することは困難です。この問題を、入力として与えられたパターンを編集する、というアプローチで解決しています。マウス操作で結果を見ながら対話的に行えます。
ORIPA(三谷 純, 2005)
※
ORIPAのWebページ
展開図の作図に特化したエディタです。角の二等分や線分の垂直二等分線など、展開図に特徴的に現れる線分の構造を簡単な操作で作図できるようにしています。また、作図した展開図が「平坦折り可能か」を判定し、平坦折り可能な場合は、折った後の予想図を表示する機能があります。一般的に、折った後の紙の重なり順は一通りだけではないので、複数のケースを列挙することも可能です。
ORI-REVO(三谷 純, 2011)
※
ORI-REVOのWebページ
軸対象な形を内部に包んだ、立体的な折り紙を設計できるソフトウェアです。軸周りに回転させる断面線を入力するだけで、あとは1枚の紙から作られることを前提に、展開図と完成予想図を自動生成します。近似的に曲面を扱えることから、従来の手作業では困難だった形が簡単に設計できます。また、軸を横切るような断面線が許容されることから、外見が複雑な形も設計できます。得られる形は対称性を持つため、幾何学的に見た目の綺麗な形が得られます。
ORI-REVO-MORPH (三谷 純, 2011)
※
ORI-REVO-MORPHのWebページ
ORI-REVOで設計された形が1枚の紙から作られる様子を可視化するアニメーションソフトウェアです。ORI-REVOで設計された形は、しばしば「本当に1枚の紙からできているの?」と疑問を持たれます。この疑問を解消するために作られました。アニメーションの中では、折り線の位置が連続的に変化するので、実際の紙の動きとは異なりますが、円筒または多角形の状態の紙から、対象とする形が作られることを確認することができます。
ORI-REF (三谷 純, 2011)
※
ORI-REFのWebページ
可展面に対して鏡映反転操作を繰り返し適用することで、立体的な折り紙形状を設計できるソフトウェアです。特定の点をマウスクリックで指定して、あとはドラッグするだけで形が得られる簡単なユーザインタフェースが特徴です。形を構成する折り線は、すべて平面曲線に限定されますが、従来の折り紙作品とは趣の異なる新しい形を試行錯誤で創り出すことが可能です。
折り紙についてさらに学ぶために
折り紙作品を鑑賞する
折り紙について学ぶ第一歩は折り紙作品を実際に自分の目で見ることだと思います。
最近の折り紙技術の進歩は目覚ましいものがあり、驚くほど精巧で、かつ芸術的な作品が世界中で作られています。その中のいくつかが、東京都文京区にある
「おりがみはうす」に展示されています。ぜひ一度足を運んで、折りの技法を間近で見てみることをお勧めします。
都内に赴くことが難しい場合はインターネット上でもさまざまな作品の写真を見ることができます。最近では、写真共有サイトである
Flickr上で折り紙作品を公開している方が多く、ちょっと覗いてみると膨大な数の折り紙の写真が見つかります。海外からの投稿が多く、
「origami」をキーワードに検索すると、いくら時間があっても見きれないほどの件数がヒットします(この原稿を執筆時現在2012年5月には26万件がヒットしました)。そのため、ある程度ターゲットを絞るために、はじめに
origamiに関するグループを検索するといいでしょう(1021件がヒットしました)。たとえば次のような、特定の分野に特化した折り紙に関するグループを見つけることができます。
・
Origami Tessellations
・
Computer Aided Origami
・
curved fold
・
Origami boxes
Flickr上では世界中の折り紙愛好家が精力的に創作活動をし、その写真を公開しながらコミュニケーションをとっています。そのエネルギーに圧倒されてしまいます。一方で、日本の折り紙作家の方々は個人のWebサイトを設けたり、ブログなどを使って作品を公開されているケースが多いようです。
小松英夫氏のWebサイトにまとめられている、国内創作家のリンク集が充実しています。
最新の情報を収集する
新しい情報を得るには研究会に参加するのが一番でしょう。折り紙に特化した研究会はあまり多く存在しませんが、年に2回、
日本折紙学会が主催する折り紙の科学・数学・教育研究集会が開催されます。また、
日本応用数理学会の中に折紙工学研究部会があり、主に折りの技術を工学的に活用する研究が発表されます。
4,5年に一度の頻度で折り紙の国際会議が開催されています。2006年に第4回(アメリカ)、2010年に第5回(シンガポール)が開催され、そして2014年に東京で第6回が開催されることになっています(
6OSMEのWebページ)。
もう少し気軽な折り紙イベントとして、日本折紙学会が主催するコンベンションや友の会(折り紙の講習会)に参加するのも選択肢の1つです。日本を代表する折り紙作家や研究者、気鋭の若手愛好家たちに会うことができます。詳しくは
日本折紙学会のWebサイトを参照ください。似た名称ですが、
日本折紙協会という団体も存在します。こちらは、折り紙の研究よりも折り紙を折って楽しむコミュニティーづくりに重点を置いているように感じます。
もちろんインターネット上でもさまざまな情報を収集できます。Flickrなどを通じてコミュニティに参加するのもよいでしょう。
国立情報学研究所が運営するCiniiでは、折り紙をキーワードに日本の論文を検索できます。
古い文献にあたる
絶版になったような古い文献を入手するのはなかなか大変です。一般的には図書館へ足を運んで探すことになるでしょうが、それでも見つからなければインターネット上のオークションで頑張って入手するというアプローチもありえるでしょう。日本折紙学会では
「折紙図書館」を運営しています。現在2000点近くの資料が管理され、第1週を除く毎週土曜日に閲覧することが可能です(詳しくは上記Webサイトの利用方法を参照ください)。
研究に役立つ書籍
- Erik D. Demaine, Joseph O’Rourke, 上原 隆平 (翻訳), 幾何的な折りアルゴリズム―リンケージ、折り紙、多面体, 近代科学社, 2009.
- Robert J. Lang, Origami Design Secrets: Mathematical Methods for an Ancient Art, Second Edition, A K Peters/CRC Press, 2011.
- Patsy Wang-Iverson, Robert J. Lang, Mark YIM, Origami 5: Fifth International Meeting of Origami Science, Mathematics, and Education, A K Peters/CRC Press, 2011.
- Robert J. Lang, Origami 4, A K Peters/CRC Press, 2009.
- Thomas Hull, 川崎 敏和, 折り紙の数理と科学, 森北出版, 2005.




























 すでに紹介した「ねじり折り(右図)」のように、紙の重なり順にサイクルを持つものもありますから、各領域に1つずつ重なり順を割り振るだけではうまくいきません。互いに重なり合う多角形領域のすべての組み合わせに対して、どちらが上でどちらが下になるのかを割り当てる必要があるのです。
すでに紹介した「ねじり折り(右図)」のように、紙の重なり順にサイクルを持つものもありますから、各領域に1つずつ重なり順を割り振るだけではうまくいきません。互いに重なり合う多角形領域のすべての組み合わせに対して、どちらが上でどちらが下になるのかを割り当てる必要があるのです。